Cuckoo Hashing

ハッシュテーブルからエントリーを検索する処理は，一般に定数時間で済むとされている。つまり，どんなにエントリーが増えても検索の速さは変わらない，ということ。データ構造の教科書には必ず載っていることだね。

でも実際には，ハッシュの衝突が起こった場合に，速度の低下が発生する可能性がある。例えば，一般的なチェイン法（オープンハッシュ）だと，衝突したエントリーに関して線形検索を行うことになるから，衝突が多ければ多いほど，定数時間からは遠のいてしまう。

この速度低下を防ぐ方法はいろいろある。なかでも cuckoo hashing （カッコウ・ハッシング）は仕組みが面白い。こいつは，エントリーの検索を必ず定数時間で済ませてくれるという優れものなんだ。

Cuckoo hashing では，２つのハッシュ関数と，２つのテーブルを用いる。ここでは，２つのハッシュ関数をそれぞれ h1, h2 として，２つのテーブルを T1, T2 としよう。

例として，ハッシュテーブルに x を挿入してみる。まず， T1 上の h1(x) が空いてるかどうかを調べる。

空いていれば，そこに x を入れてしまう。

空いてない場合はどうする？ 例えば y が先に入っているとしよう。

そういう場合は， y を追い出して x を突っ込んでしまう。「x と y をスワップする」といった方がいいかもしれない。

次に，T2 上の h2(y) が空いてるかどうかを調べる。

空いていれば，そこに y を入れてしまう。

空いてない場合はどうするか？ 例えば z が先に入っているとしよう。

そういう場合は， z を追い出して y を突っ込んでしまう。

そして，T1 上の h1(z) が空いてるかどうかを調べる。

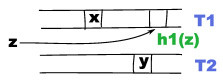
空いていれば，そこに z を入れて，空いてなければ，それを追い出して z を入れて……というように，「先約がいたら追い出して，追い出されたやつをもう一方のテーブルに突っ込んで」という処理を，全部がどこかに納まるまで繰り返す。

こうしてできたテーブルでは， x は T1[h1(x)] か T2[h2(x)] のどちらかに入っていることが保証される。つまり，この２つを探すだけで，必ず x を見つけることができるというわけ。

挿入処理の擬似コードは以下のようになる。

この擬似コードを見てみると，ループ回数に制限を設けていることが分かると思う。「全部がどこかに納まるまで繰り返す」と書いたけれど，実は循環参照が生じると無限ループに陥ってしまう可能性があるんだ。だから実際には，適当な回数ループしてしまったら潔く諦めて，ハッシュ関数を取り替えたうえでテーブルの再構築を行うようにしている。この再構築のコストが cuckoo hashing における最大の弱点といえる。

……と，こんな感じの cuckoo hashing, 見ての通り挿入処理にかなりのクセがあるのだけれど，検索が必ず固定時間で終わるというのは面白い。ちょっと怖くて自分で使う気にはなれないけどね。なにかのときのために名前だけは覚えておくよ。